数据结构第二章-线性表

数据结构第二章线性表

计算机学科基础：数据结构第二章线性表的学习笔记

1.线性表的定义

①定义：具有相同数据类型的n个数据元素的有限序列，线性表是一种逻辑结构，表示元素之间一对一的相邻关系
②特点：表中的元素在逻辑上相邻，具有逻辑上的顺序性，有其先后次序，每个元素只有唯一的前驱元素

2.顺序表（线性表的顺序存储结构✪）

①定义：线性表的顺序存储又称顺序表，它是用一组地址连续的存储单元依次存储线性表中的数据元素
从而使得逻辑上相邻的两个元素在物理位置上也相邻
②特点
- 顺序表中元素的逻辑顺序与其物理顺序相同
- 顺序表中的任意一个数据元素都可以随机存取，即通过首地址和元素序号可在时间O(1)内找到指定的元素。
- 顺序表的存储密度高，每个结点只存储数据元素。
- 顺序表逻辑上相邻的元素物理上也相邻，所以插入和删除操作需要移动大量元素。
- n个元素的顺序表可插入的位置有n+1个，移动次数总数为：n(n+1)/2
  平均移动次数为：n/2
- n个元素的顺序表删除元素时，平均移动次数为：(n-1)/2
- n个元素的顺序表顺序查找的平均比较/查找次数为：(n+1)/2

③代码实现（用数组来描述线性表的顺序存储结构♚）

顺序表的定义

静态分配一维数组

#define MaxSize 50 //定义顺序表的最大长度
typedef struct{
    int data[Maxsize]; //顺序表的元素
    int length; //顺序表的当前长度
}SqList;

void InitList(SqList &L)//对顺序表进行初始化 
{
	for(int i=0;i<MaxSize;i++)
	{
		L.data[i]=0;
	}
	L.length=0;
}

动态分配一维数组（存储数组的空间使用malloc函数进行动态分配）

#define InitSize 100 //默认的最大长度
typedef struct{
	int *data; //指示动态分配数组的指针
	int MaxSize,length; //数组的最大容量和当前顺序表的长度
}SeqList;

int main()
{
    SeqLsit L;
	InitList(L); //初始化顺序表
    //...向表中插入几个元素
    IncreaseSize(L,5)
    return 0;    
}

void InitList(SeqList &L)//使用动态分配方法的初始化
{
    L.data=(int *)malloc(InitSize*sizeof(int));//用malloc函数申请一片连续的存储空间
    L.length=0;
    L.MaxSize=InitSize;
}

void IncreaseSize(SeqList &L,int len)//为数组分配新的空间
{
    int *p=L.data;//申请一个新指针
    L.data=(int *)malloc((L.MaxSize+len)*sizeof(int));
    for(int i=0;i<L.length;i++)
    {
        L.data[i]=p[i];
    }
    L.MaxSize=L.Maxsize+len;
    free(p);//释放原来的内存空间
}

顺序表的插入操作（平均时间复杂度：O(n)）

int Insert(SqList &L,int i,int e)//顺序表的插入，指定位置，插入元素 
{
	if(i<1||i>L.length+1)
		return 0;
	if(L.length>=MaxSize)
		return 0;
	for(int j=L.length;j>=i;j--)
		L.data[j]=L.data[j-1];
	L.data[i-1]=e;
	L.length++;
	return 1; 
}

顺序表的删除操作（平均时间复杂度：O(n)）

int Delete(SqList &L,int i,int &e)//顺序表的删除，删除指定位置的元素，并传出此元素 
{
	if(i<1||i>L.length)
		return 0;
	e=L.data[i-1];
	for(int j=i;j<L.length;j++)
		L.data[j-1]=L.data[j];
	L.length--;
	return 1;
}

顺序表的按值查找位置（平均时间复杂度：O(n)）

int Locate(SqList L,int e)//按值查号，返回该第一个等于值的位置 
{
	for(int i=0;i<L.length;i++)
		if(L.data[i]==e)
			return i+1; //查到了则返回其位序
	return 0; 
}

顺序表的按位查找元素（平均时间复杂度：O(1)，此时为随机访问）

int Get(SqList L,int i,int &e)//按位查找，返回在位置i上的元素e 
{
	if(i<1||i>L.length)
		return 0;
	e=L.data[i-1];
	return 0; 
}

3.链表（线性表的链式存储结构✪）

①定义：线性表的链式存储又称单链表，它是指通过一组任意的存储单元来存储线性表中的数据元素。
为了建立数据元素之间的线性关系，对每个链表结点，除存放元素自身的信息外，还需要存放一个指向其后继的指针。
②特点
- 链式存储线性表时，不需要使用地址连续的存储单元，不要求逻辑上相邻的元素在物理上也相邻
- 插入和删除元素不需要移动元素，只需要修改指针。
- 单链表附加指针域，也存在浪费存储空间的缺点。
- 由于单链表的元素离散地分布在存储空间中，所以单链表是非随机存取的存储结构，
  即不能直接找到表中某个特定的结点。查找某个特定的结点时，需要从表头开始遍历，依次查找。
- 设一个有序的单链表中有n个结点，现要求插入一个新节点后使得单链表仍然保持有序，则该操作的时间复杂度为O(n)

③代码实现（♚）

单链表的定义

单链表的结点由数据域（data，存放数据元素）和指针域（next，存放其后继结点的地址）组成

typedef struct LNode{
	int data; //数据域
	struct LNode *next; //指针域
}LNode, *LinkList; //别名，第一个强调它是一个结点，第二个强调它是一个链表

// 注：要表示一个单链表，只需声明一个头指针L，指向单链表的第一个结点。
// LNode *L;或 LinkList L;

初始化单链表

带头结点的单链表（头指针指向头结点）

图片
为了操作上的方便，在单链表第一个结点之前附加一个结点，称为头结点
头结点的数据域不带任何信息，指针域指向线性表的第一个数据结点（区分第一个结点和第一个数据结点）
头结点和头指针的区分：不管带不带头结点，头指针都始终指向链表的第一个结点
而头结点是带头结点的链表中的第一个结点，结点内通常不存储信息。
引入头结点的优点
- 对于插入或删除第一个数据结点的操作，由于第一个数据结点的位置被存放在头结点的指针域中，
  因此在链表的第一个位置上的操作和在表的其他位置上的操作一致，无须进行特殊处理。
- 无论链表是否为空，其头指针都是指向头结点的非空指针（空表中头结点的指针域为空）
  因此空表和非空表的处理也就得到了统一。

代码实现

int InitList(LinkList &L)//初始化单链表 
{
	L=(LNode *)malloc(sizeof(LNode));//分配一个头结点 
	if(L==NULL)
		return 0;
	L->next=NULL; //头结点之后暂时还没有结点
	return 1; 
}

不带头结点的单链表（头指针指向第一个数据结点）
1
2
3
4
5
int InitList(LinkList &L)
{
L=NULL;
return 1;
}

建立单链表

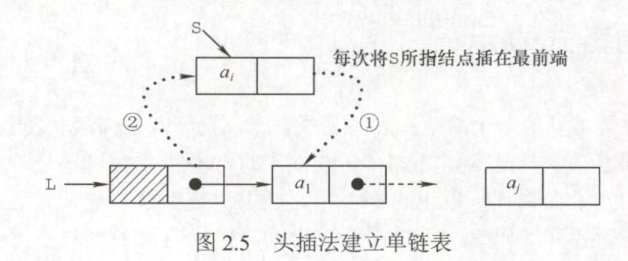
使用头插法建立单链表（时间复杂度O(n)）

图片
从一个空表开始，生成新结点，并将读取到的数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头
读入数据的顺序与生成的链表中的元素的顺序是相反的

代码实现

LinkList List_HeadInsert(LinkList &L)//头插法建立单链表,可以用于实现逆置 
{
	LNode *s;
	int x;
	L=(LinkList)malloc(sizeof(LNode)); //创建头结点
	L->next=NULL;   //初始为空链表
	scanf("%d",&x);
	while(x!=9999)
	{
		s=(LNode*)malloc(sizeof(LNode)); //创建新结点
		s->data=x;
		s->next=L->next;
		L->next=s;  //将新结点插入表中，L为头指针
		scanf("%d",&x); 
	} 
	return L; 
}

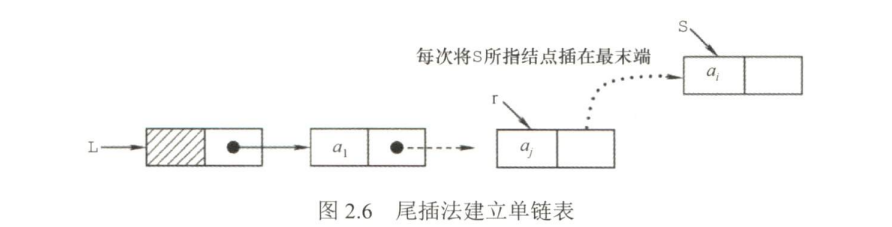
使用尾插法建立单链表（时间复杂度O(n)）

图片
该方法将新结点插入到当前链表的表尾，需要增加一个尾指针r，使其始终指向当前链表的尾结点

代码实现

LinkList List_TaliInsert(LinkList &L)//尾插法建立单链表 
{
	int x;
    
	L=(LinkList)malloc(sizeof(LNode));
	LNode *s,*r=L;		//尾插法需要建立一个尾指针r,刚开始都指向头结点 
	scanf("%d",&x);
	while(x!=9999)
	{
		s=(LNode *)malloc(sizeof(LNode));
		s->data=x;
		r->next=s;
		r=s;
		scanf("%d",&x); 
	} 
	r->next=NULL;	//尾结点指针置空
	return L; 
}

单链表按序号查找结点（时间复杂度O(n)）

LNode *GetElem(LinkList L,int i)//循环单链表找到第i个位置的指针 
{
    if(i<1)
        return NULL;	//若i无效，返回NULL
	int j=0;	//相当于把头结点看作是0号位置
	LNode *p=L;	//刚开始P指向头结点
	while(p!=NULL&&j<i)
	{
		p=p->next;
		j++;	
	}
	return p; //返回第i个结点的指针，若i大于表长，则返回NULL
}

单链表按值查找节点（时间复杂度O(n)）

LNode *LocateElem(LinkList L,int e)//按值查找结点 
{
	LNode *p=L->next;
	while(p!=NULL&&p->data!=e)	//从第一个结点开始查找数据域为e的结点
	 	p=p->next;
	return p; 	//找到后返回该结点的指针，如果链表中没有该值将返回空值 
}

单链表的插入结点操作

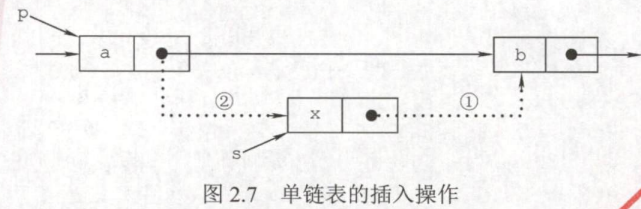
指定的结点后插操作

查找待插入位置的前驱结点的时间复杂度为O(n)，在给定的结点后面插入新结点的时间复杂度为O(1)
图片
插入结点操作将值为×的新结点插入到单链表的第i个位置上。先检查插入位置的合法性
然后找到待插入位置的前驱结点，即第i-1个结点，再在其后插入新结点
算法首先调用按序号查找算法GetElem（L，i-1），查找第i-1个结点。
假设返回的第i-1个结点为p，然后令新结点s的指针域指向p的后继结点，再令结点p的指针域指向新插入的结点s

代码实现

p=GetElem(L,i-1); //查找插入位置的前驱结点
，，，
int InsertNext(LNode *p,int e)//指定结点的后插操作,需要找到其前驱结点,此时的p是指向待插入位置的前驱结点的指针  
{
	if(p==NULL)
		return 0;
	LNode *s=(LNode *)malloc(sizeof(LNode));
	s->data=e;
	s->next=p->next; 
	p->next=s;
	return 1;
}

指定结点的前插操作

查找待插入位置的结点的时间复杂度为O(n)，在给定的结点前面插入新结点的时间复杂度为O(1)

p=GetElem(L,i-1); //查找待插入位置的结点
，，，
int InsertPrior(LNode *p,int e)
{
	if(p==NULL)
		return 0;
	LNode *s=(LNode *)malloc(sizeof(LNode));
	s->next=p->next; 
	p->next=s;
	s->data=p->data;  //交换了数据域 
	p->data=e; 
	return 1;
}

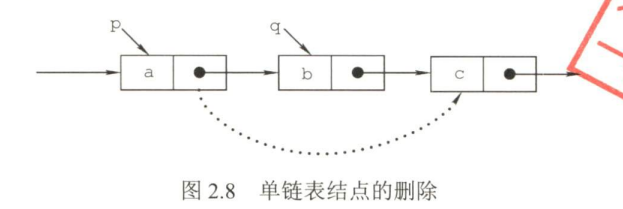
单链表的删除结点操作

寻找待删除结点的前驱结点，再执行相关删除操作

查找待删除位置的前驱结点的时间复杂度为O(n)，删除此结点的时间复杂度为O(1)
图片
先检查删除位置的合法性，后查找表中第i-1个结点，即被删结点的前驱结点，再将其删除

代码实现

int Delete(LinkList &L,int i,int &e)//删除第i个位置的元素，并用e返回删除元素的值,需要找到前驱结点 
{
	if(i<1)
		return 0;
	LNode *p=GetElem(L,i-1);	//循环单链表找到第i-1个位置的指针
	if(p==NULL)
		return 0;
	if(p->next==NULL)
		return 0;
	LNode *q=p->next;	//新创建一个指针，并使该指针指向当前欲删除的结点 
	e=q->data;
	p->next=q->next;	//修改前驱结点的指针域使其指向待删除结点的下一个结点,将*q结点从链中断开 
	free(q);	//释放结点的存储空间 
	return 1; 
}

寻找待删除结点，再执行相关删除操作

查找待删除位置的结点的时间复杂度为O(n)，删除此结点的时间复杂度为O(1)

删除结点P的操作可用删除P的后继结点操作来实现，实质就是将其后继结点的值赋予其自身，然后删除后继结点

p=GetElem(L,i-1); //查找待插入位置的结点
，，，
int DeleteNext(LNode *p,int &e)//删除需删除结点的后继结点，但是此时由于该原本该删除的结点的数据域和指针域已经被实际删除的结点的值覆盖，因此相当于删除了需删除的结点 
{
	if(p==NULL)
		return 0;
	LNode *q=p->next;
    e=p->data;
	p->data=q->data;
	p->next=q->next
	free(q);
	return 1;
}

单链表的求表长操作（时间复杂度为O(n)）
- 求表长操作就是计算单链表中数据结点（不含头结点）的个数，需要从第一个结点开始顺序依次访问表中的每个结点，
  为此需要设置一个计数器变量，每访问一个结点，计数器加1，直到访问到空结点为止。
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  void Length(LinkList L)//求表长
  {
  int j=0;
  LNode *p=L->next; //创建一个指针指向第一个数据结点
  while(p!=NULL)
  {
  j++;
  p=p->next;
  }
  printf("%d\n",j);
  }

4.双链表（主要考察选择题✪）

①定义
- 双链表结点中有两个指针prior和next，分别指向其前驱结点和后继结点，
  在指针已经指向相应结点的情况下，插入和删除的时间复杂度为O(1)
- 图片

②代码实现

双链表的定义

typedef struct DNode{
	int data;
	struct DNode *prior,*next;
}; DNode,*DLinkList;

双链表的初始化

int InitDLink(DLinkList &L)
{
	L=(DNode *)malloc(sizeof(DNode));
	if(L==NULL)
		return 0;
	L->prior=NULL;//头结点的前驱指针永远指向NULL 
	L->next=NULL;
	return 1;
}

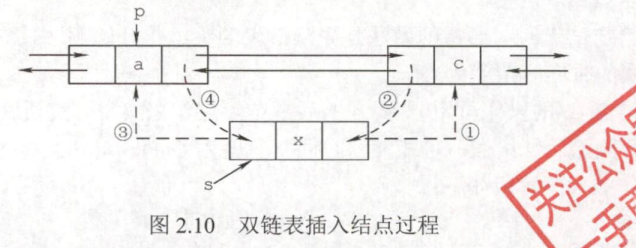
双链表的插入操作

图片

int Insert(DNode *p,DNode *s)//在i位置上的p节点之后插入结点s，数值为e 
{
    if(p==NULL||S==NULL)
        return 0;
	s->next=p->next; //1
	if(p->next!=NULL)
		p->next->prior=s;
	s->prior=p;  //2
	p->next=s; 	 //3
	p->data=e;	 //4
	return 1; 
} //1和2步必须在第4步之前，否则p的后继结点的指针就会丢掉，导致插入失败

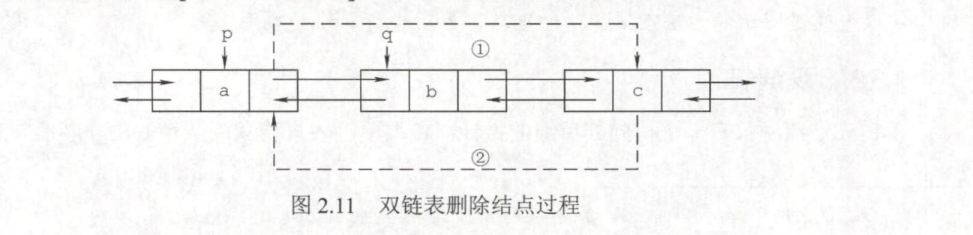
双链表的删除操作

图片

int Delete(DNode *p)//删除p结点的后继结点q 
{	
	if(p==NULL)
		return 0;
	DNode *q=p->next; //找到p的后继结点q 
	if(q==NULL)//p结点没有后继 
		return 0;
	p->next=q->next; 
	if(q->next!=NULL)
		q->next->prior=p;
	free(q);
	return 1; 
}

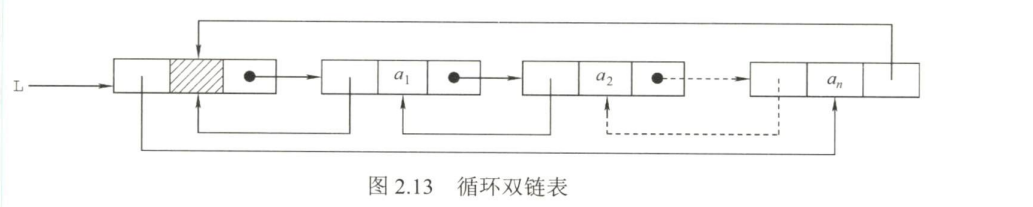
5.循环链表（主要考察选择题✪）

①循环单链表
- 图片
- 循环单链表和单链表的区别在于，表中最后一个结点的指针不是NULL，而改为指向头结点，从而整个链表形成一个环
- 在循环单链表中，表尾结点r的next域指向L，故表中没有指针域为NULL的结点，
  因此，循环单链表的判空条件不是头结点的指针是否为空，而是它是否等于头指针。
- 在单链表中只能从表头结点开始往后顺序遍历整个链表，而循环单链表可以从表中的任意一个结点开始遍历整个链表
- 有时对循环单链表不设头指针而仅设尾指针，以使得操作效率更高。
  - 其原因是，若设的是头指针，对在表尾插入元素需要O(n)的时间复杂度，
  - 而若设的是尾指针r，r->next即为头指针，对在表头或表尾插入元素都只需要O($1$)的时间复杂度。
②循环双链表
- 图片
- 循环双链表中，头结点的前指针指向表尾节点，判空的条件是头结点的前后指针域都等于头结点
- 循环双链表是有助于删除第一个结点、删除最后一个结点，在第一个结点前插入一个结点，在最后一个结点后添加一个结点
  - 选A、C，如果是循环单链表，没办法处理删除最后一个结点（无法快速找到最后一个结点的前驱结点）

6.静态链表

静态链表借助数组来描述线性表的链式存储结构，也有指针域和数据域
- 图片
指针表示下一个元素的数组下标（游标），静态链表也需要事先分配一块连续的内存空间。
其插入和删除不需要移动元素，只需要修改指针。
以next==-1作为结束的标志。

代码实现

#define MaxSize 50
typedef struct{
    int data;
    int next;
}SLinkList[MaxSize];

7.顺序表和链表的比较（✪）

1.存取（读写）方式
- 顺序表可以顺序存取，也可以随机存取，链表只能从表头顺序存取元素。
- 例如在第i个位置上执行存或取的操作，顺序表仅需一次访问，而链表则需从表头开始依次访问i次。
2.逻辑结构与物理结构
- 采用顺序存储时，逻辑上相邻的元素，对应的物理存储位置也相邻。
- 而采用链式存储时，逻辑上相邻的元素，物理存储位置不一定相邻，对应的逻辑关系是通过指针链接来表示的。
3.查找、插入和删除操作
- 对于按值查找，顺序表无序时，两者的时间复杂度均为O(n)
  顺序表有序时，可采用折半查找，此时的时间复杂度为O($log_2n$).
- 对于按序号查找，顺序表支持随机访问，时间复杂度仅为O(1)
  而链表的平均时间复杂度为O(n)
- 顺序表的插入、删除操作，平均需要移动半个表长的元素。
  链表的插入、删除操作，只需修改相关结点的指针域即可。
- 由于链表的每个结点都带有指针域，故而存储密度不够大。
4.空间分配
- 顺序存储在静态存储分配情形下，一旦存储空间装满就不能扩充，若再加入新元素，则会出现内存溢出，
  因此需要预先分配足够大的存储空间。
  - 预先分配过大，可能会导致顺序表后部大量闲置；
  - 预先分配过小，又会造成溢出。
- 动态存储分配虽然存储空间可以扩充，但需要移动大量元素，导致操作效率降低，
  而且若内存中没有更大块的连续存储空间，则会导致分配失败。
- 链式存储的结点空间只在需要时申请分配，只要内存有空间就可以分配，操作灵活、高效。
如何选取存储结构
- 1.基于存储的考虑
  - 难以估计线性表的长度或存储规模时，不宜采用顺序表
  - 链表不用事先估计存储规模，但链表的存储密度较低，显然链式存储结构的存储密度是小于1的。
- 2.基于运算的考虑
  - 在顺序表中按序访问的时间复杂度为O(1)，而链表中按序号访问的时间复杂度为O(n),
    因此若经常做的运算是按序号访问数据元素，则显然顺序表优于链表。
  - 在顺序表中进行插入、删除操作时，平均移动表中一半的元素，当数据元素的信息量较大且表较长时，这一点是不应忽视的
  - 在链表中进行插入、删除操作时，虽然也要找插入位置，但操作主要是比较操作，从这个角度考虑显然后者优于前者。
- 3.基于环境的考虑
  - 顺序表容易实现，任何高级语言中都有数组类型，链表的操作是基于指针的，
    相对来讲，前者实现较为简单，这也是用户考虑的一个因素。
  - 通常较稳定的线性表选择顺序存储，而频繁进行插入、删除操作的线性表（即动态性较强）宜选择链式存储。