数据结构第三章-栈,队列和数组

数据结构第三章-栈，队列和数组

计算机学科基础：第三章栈，队列和数组的学习笔记

1.栈（✪）

栈的基本概念（操作受限的线性表）

• 栈的定义：只允许在一端进行插入或删除操作的线性表
• 栈顶是允许进行插入删除操作的那一端
• 栈的特点：后进先出
• 卡特兰数：n个不同元素进栈，出栈元素的不同排列的个数为： $(\frac{1}{n+1})*C_{2n}^n$
• 无论是顺序栈还是链栈，出入栈的时间复杂度都为O(1)

顺序栈（✪）

• 概念：采用顺序存储的栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，
  同时附设一个指针(top)指示当前栈顶元素的位置。

• 指针的变化（具体问题具体分析）

  • 指针的设置：S.top，初始时设置S.top=-1，栈顶元素：S.data[S.top]
  • 进栈操作：栈不满时，栈顶指针先加1，再送值到栈顶元素
  • 出栈操作：栈非空时，先取栈顶元素值，再将栈顶指针减1
  • 栈空条件：栈空条件：S.top\==-1
  • 栈满条件：S.top==MaxSize-1；栈长：S.top+1

• 代码表示

  • 顺序栈的定义

    #define MaxSize 50
    typedef struct{
    	int data[MaxSize];
    	int top;//栈顶指针，指示当前栈顶元素的位置 
    }SqStack;

  • 顺序栈的初始化

    void InitStack(SqStack &S)//初始化 
    { 
    	S.top=-1; //初始化栈顶指针 
    } 

  • 顺序栈的判空

    bool StackEmpty(Sqstack S)//判空 
    {
    	if(S.top==-1)
    		return true;
    	else
    		return false;
    } 

  • 顺序栈的进栈

    bool Push(SqStack &S,int x)//进栈 
    {
    	if(S.top==MaxSize-1)
    		return false; 
    	S.data[++S.top]=x; //此处表示当栈不满时，先加栈顶指针，再执行进栈操作 
    	return true; 
    }

  • 顺序栈的出栈

    bool Pop(SqStack &S,int &x)//出栈
    {
    	if(S.top==-1)
    		return false;
    	x=S.data[S.top--];//此时表示当栈不为空时，先将指针处元素赋予x,再将栈顶指针减一，执行出栈操作 
    	return true; 
    } 

  • 读取栈顶的元素

    bool GetTOP(SqStack S,int &x)//读栈顶元素 
    {
    	if(S.top==-1)
    		return false;
    	x=S.data[S.top];
    	return true; 
    }

  • 注意事项

    • 若栈顶指针初始化为S.top=0，即top指向栈顶元素的下一位置，
    • 则入栈操作变为S.data[S.top++]=x；
    • 出栈操作变为x=S.data[—S,top]；

• 关于共享栈（非重点）

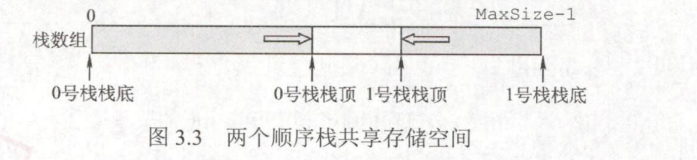
  • 共享栈的定义：利用栈底位置相对不变的特性，可让两个顺序栈共享一个一维数组空间，
    将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸
  • 图片
    • 
  • 共享栈的栈顶指针
    • 两个栈的栈顶指针都指向栈顶元素，top0=-1时0号栈为空，top1=MaxSize时1号栈为空；
    • 仅当两个栈顶指针相邻(top1-top0=1)时，判断为栈满
  • 共享栈的出入栈操作：当0号栈进栈时top0先加1再赋值，1号栈进栈时top1先减1再赋值；出栈时则刚好相反。
  • 共享栈的特点：共享栈是为了更有效地利用存储空间，两个栈的空间相互调节，
    只有在整个存储空间被占满时才发生上溢，对存取效率没有影响

链式栈（✠）

• 链栈的定义：链栈一般由单链表来实现，不带头节点，并规定所有的操作都在表头来进行（相当于栈顶），头指针指向栈顶元素。

• 链栈的优点：链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况

• 图片

  • 

• 代码实现

  • 链栈的定义

    typedef struct Linknode {
    	int data;	//数据域
    	struct Linknode *next;	//指针域 
    }*LiStack;

  • 链栈的初始化

    void InitStack(LiStack &S)//初始化链栈 
    {
     	S=NULL;//头指针为空
    } 

  • 链栈的入栈

    bool Push(LiStack &S,int x)//入栈操作 
    {
      Linknode *p=(Linknode *)malloc(sizeof(Linknode));//分配了一个结点的空间 
      p->data=x;
      p->next=S; 
      S=p; 
      return 0;	 
    } 

  • 链栈的出栈

    bool Pop(LiStack &S,int &x)//出栈操作
    {
     if(S==NULL)
        return false;	
     x=S->data;
     S=S->next;
     return true; 	 
    } 

  • 链栈的判空

    bool EmptyStack(LiStack S)//判空
    {
     if(S==NULL)
       return true;
     else
      return false; 
    } 

  • 取栈顶元素

    bool GetTOP(LiStack S,int &x)//取栈顶元素
    {
      if(S==NULL)
        return false;	
      x=S->data;
      return true; 	 
    }

2.队列（✪）

队列的基本概念（操作受限的线性表）

• 队列的定义：只允许在表的一端进行插入，而在表的另一端进行删除。
• 向队列中插入元素称为入队或进队（此端为队尾rear）；删除元素称为出队或离队（此端为队头front）
• 特点：先进先出

顺序队列

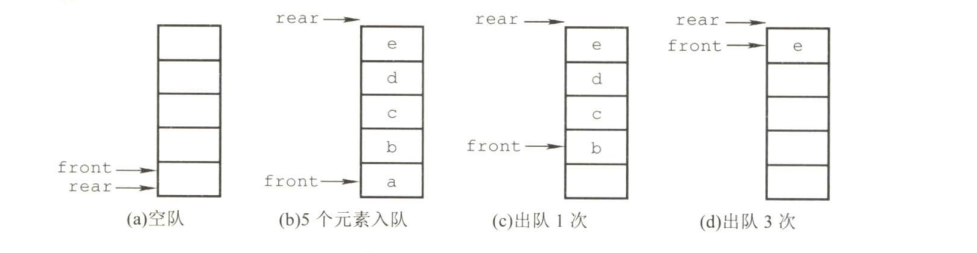
• 顺序队列的指针设置：顺序队列设置两个指针，队头指针front指向队头元素，队尾指针rear指向队尾元素的下一个位置

• 顺序队列的出入队操作

  • 进队操作：队不满时，先送值到队尾元素，再将队尾指针加一
  • 出队操作：队不空时，先取队头元素值，再将队头指针加一

• 初始时：Q.front==Q.rear\==0，此即为判空的条件

• 存在的问题：不能用 Q.rear==MaxSize作为判断队满的条件，并且还有可能造成假溢出

• 图片

  • 

• 代码实现

  typedef struct{
  	int data[MaxSize];
  	int front,rear; //队头指针指向队头元素、队尾指针指向队尾元素的下一个位置 
  }SqQueue;

循环队列（✪）

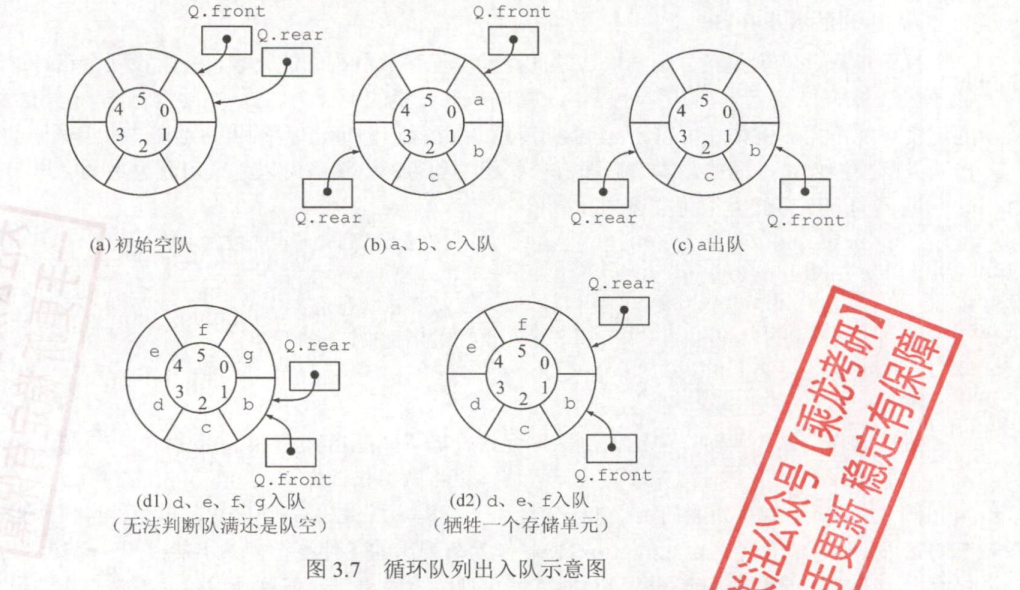
• 循环队列的概念：采用循环队列时，将顺序队列想像成一个环形的空间（逻辑上视为一个环），
  当队首指针Q.front==MaxSize-1后，再前进一个位置就自动到0，可采取除法取余运算（%）来实现。

• 循环队列的指针设置：入队出队时相应的指针按顺时针方向进1

  • 初始时：Q.front=Q.rear=0
  • 出队时，队首指针进1：Q.front=(Q.front+1)%MaxSize.
  • 入队时，队尾指针进1：Q.rear=(Q.rear+1)%MaxSize.
  • 队列长度：(Q.rear+MaxSize-Q.front)%MaxSize.

• 循环队列的判空条件：Q.front==Q.rear。

• 此时的局限性：若入队元素的速度快于出队元素的速度，则队尾指针很快就会赶上队尾指针，此时将无法判断队满还是队空

• 三种处理方式区分队空和队满的判断条件（✪）

  • 牺牲一个数组单元来区分队空和队满（♚）

    • 具体实现：入队时少用一个队列单元，约定以“队头指针在队尾指针的下一位置“作为队满的标志

    • 此时判断队满和队空的条件

      • 队满条件：(Q.rear+1)%Maxsize\==Q.front
      • 队空条件：Q.front==Q.rear.
      • 队列中元素的个数：(Q.rear-Q.front+MaxSize)%MaxSize。
    • 图片
      • 
    • 例题：本题选A
      • 

  • 结构体类型中增设表示元素个数的数据成员（size）

    • 入队时：Q.size++；出队时：Q.size—，此时队空和队满都满足：Q.front\==Q.rear
    • 队空的条件为：Q.s1ze\==0
    • 队满的条件为：Q.size\==MaxSize

  • 结构体类型中增设tag数据成员，以区分是队满还是队空。

    • 初始化时tag=0；入队成功时令tag=1；出队成功时令tag=0
    • tag等于0时，若因删除导致Q.front\==Q.rear,则为队空
    • tag等于1时，若因插入导致Q.front\==Q.rear,则为队满

• 循环队列的代码实现

  • 循环队列的初始化

    void InitQueue(SqQueue &Q)//初始化 
    {
    	Q.rear=Q.front=0;	//初始化队首与队尾指针 
    } 

  • 循环队列的判断队空

    bool Empty(SqQueue Q)//判空 
    {
    	if(Q.rear==Q.front) 
    		return true;
    	else
    		return false; 
    } 

  • 循环队列的入队

    bool EnQueue(SqQueue &Q,int x)//入队 
    {
    	if((Q.rear+1)%MaxSize==Q.front)	//判断队列是否已满	
    		return false;
    	Q.data[Q.rear]=x;
    	Q.rear=(Q.rear+1)%MaxSize;
    	return true; 
    } 

  • 循环队列的出队

    bool DeQueue(SqQueue &Q,int &x)//出队
    {
    	if(Q.rear==Q.front)	//判空 
    		return false; 
    	x=Q.data[Q.front];
    	Q.front=(Q.front+1)%MaxSize;
    	return true; 
    } 

  • 取循环队列的队首元素

    bool GetHead(SqQueue Q,int &x)//出队
    {
    	if(Q.rear==Q.front)//判空 
    		return false; 
    	x=Q.data[Q.front];
    	return true; 
    } 

链式队列（✠）

• 链式队列的定义

  • 一个同时带有队头指针和队尾指针的单链表。头指针指向队头结点，尾指针指向队尾结点(即单链表的最后一个结点)
    注意与顺序存储的不同
  • 一般将链式队列设计成一个带头结点的单链表，统一插入和删除操作
  • 最适合作为链队的链表是带队头指针和队尾指针的非循环单链表（带头结点），
    此时可快速在第一个位置实现删除操作，在最后一个位置实现插入操作（循环单链表画蛇添足了）
  • 用链式方式存储的队列，在进行插入运算时，头尾指针可能都要修改
    • 当队列不为空时，只会修改rear尾指针。
    • 当队列为空时，再当有头结点时，也只要修改rear
    • 当队列为空且没有头结点时，头尾指向相同，在插入时就需要同时修改头和尾

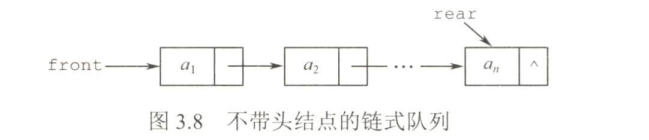
• 不带头结点的链式队列

  • 图片
    • 
  • 链式队列的判空：当Q.front\==NULL&&Q.rear==NULL时，链式队列为空
  • 链式队列的出入队操作：
    • 入队时，建立一个新结点，将新结点插入到链表的尾部，并让Q.rear指向这个新插入的结点
      若原队列为空队，则令Q.front也指向该结点
    • 出队时，首先判断队是否为空，若不空，则取出队头元素，将其从链表中摘除，并让Q.front指向下一个结点
      若该结点为最后一个结点，则置Q.front和Q.rear都为NULL

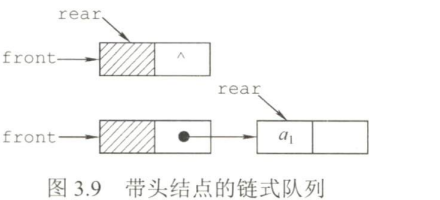
• 带头结点的链式队列

  • 图片
    • 
  • 链式队列的判空：Q.front==Q.rear
  • 链式队列的出入队操作
    • 入队时，建立一个新结点，将新结点插入到链表的尾部，并让Q.rear指向这个新插入的结点
    • 出队时，首先判断队是否为空，若不空，则取出队头元素，将其从链表中摘除，并让Q.front指向下一个结点
      若该结点为最后一个结点，则置Q.rear=Q.front

• 链式队列的优点

  • 用单链表表示的链式队列特别适合于数据元素变动比较大的情形，而且不存在队列满且产生溢出的问题。
  • 假如程序中要使用多个队列，与多个栈的情形一样，最好使用链式队列，这样就不会出现存储分配不合理和“溢出”的问题。

• 带头结点的链式队列的代码实现

  • 链式队列的定义

    typedef struct LinkNode//链式队列结点 
    {
    	int data;
    	struct LinkNode *next;
    }LinkNode;
    
    typedef struct//链式队列 
    {
    	LinkNode *front,*rear;//链式队列头指针与尾指针 
    }LinkQueue;  

  • 链式队列的初始化

    void InitQueue(LinkQueue &Q)//链式队列的初始化 
    {
    	Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));//头指针和尾指针指向新建立的头结点 
    	Q.front->next=NULL;//初始为空 
    } 

  • 链式队列的判空

    bool Empty(LinkQueue Q)//链式队列的判空 
    {
    	if(Q.front==Q.rear)
    		return true;
    	else
    		return false;
    } 

  • 链式队列的入队

    void EnQueue(LinkQueue &Q,int x)//链式队列的入队 
    {
    	LinkNode *s=(LinkNode *)malloc(sizeof(LinkNode));//创建新节点 
    	s->data=x;
    	s->next=NULL;
    	Q.rear->next=s;
    	Q.rear=s;
    } 

  • 链式队列的出队

    //用链式存储方式的队列进行删除操作时需要：头尾指针可能都需要修改,因为如果此时队列中只有一个元素的话，删除之后，队列为空，需要将Q.rear=Q.front;
    bool DeQueue(LinkQueue &Q,int &x)//链式队列的出队 
    {
    	if(Q.front==Q.rear)//判空 
    		return false;
    	LinkNode *p=Q.front->next;	//创建一个指针此时指向出队的结点 
    	x=p->data;
    	Q.front->next=p->next;	//进行出队的操作
    	if(Q.rear==p)//	若原队列中只有一个结点，则删除之后变空。 
    		Q.rear=Q.front;
    	free(p);
    	return true; 
    }	

双端队列（主要考察选择题✪）

• 双端队列的概念：双端队列是指允许两端都可以进行入队和出队操作的队列，此时可以加上一定的限制
  形成输出受限的双端队列和输入受限的双端队列
• 题目考查
  • 作为选择题：常常以输入序列来判断相关的输出序列是否正确，此时的方法是画图进行分析。
  • 特别地，对于输出序列受限的这一类的题目，可以将其的输出序列直接依次填入所画的双端队列图，由题目的输入序列来反推是否可以得到此输出序列
  • 例题：分别选C、C
    • 

3.栈和队列的应用 (侧重手算模拟,代码不需要掌握✪)

栈在括号匹配中的应用

• 过程：依次扫描所有字符，遇到左括号入栈，遇到右括号则弹出栈顶元素检查是否匹配。
• 匹配失败情况：①左括号单身②右括号单身③左右括号不匹配
• 流程图
  • 
• 算法实现
  • 

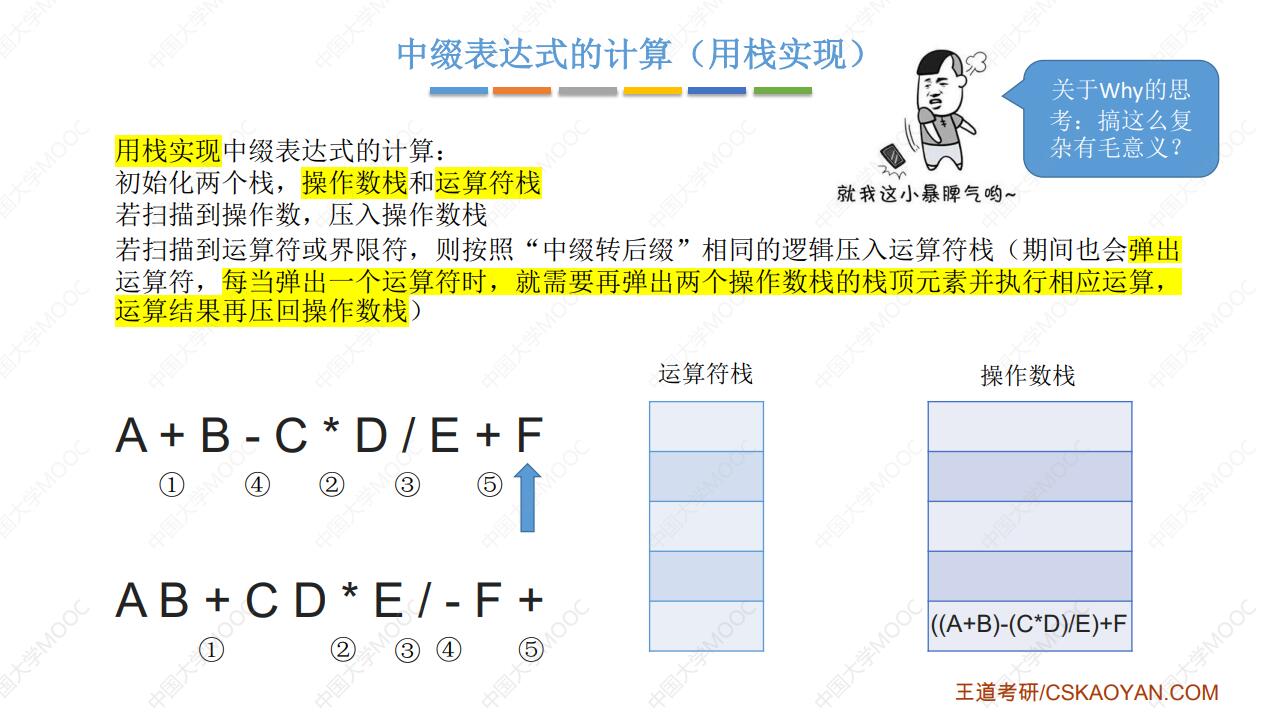
栈在表达式求值中的应用（✪）

• 中缀表达式
  • 中缀表达式包括:操作数、运算符、界限符
  • 其运算符在两个操作数的中间（a+b-c*d）
  • 图片
    • 
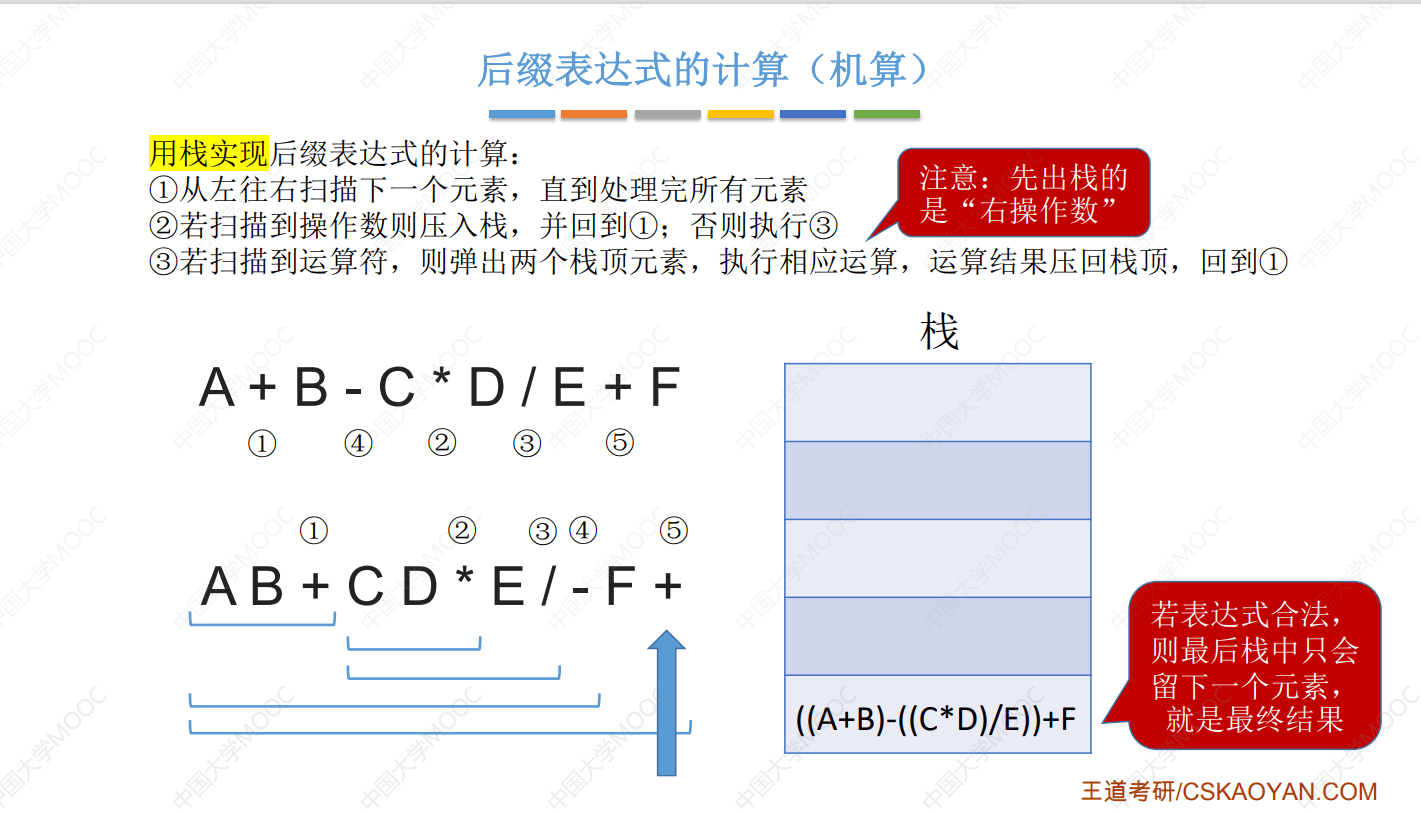
• 后缀表达式（♚）
  • 定义：也称逆波兰表达式，运算符在两个操作数的后面（$ab+cd*-$）
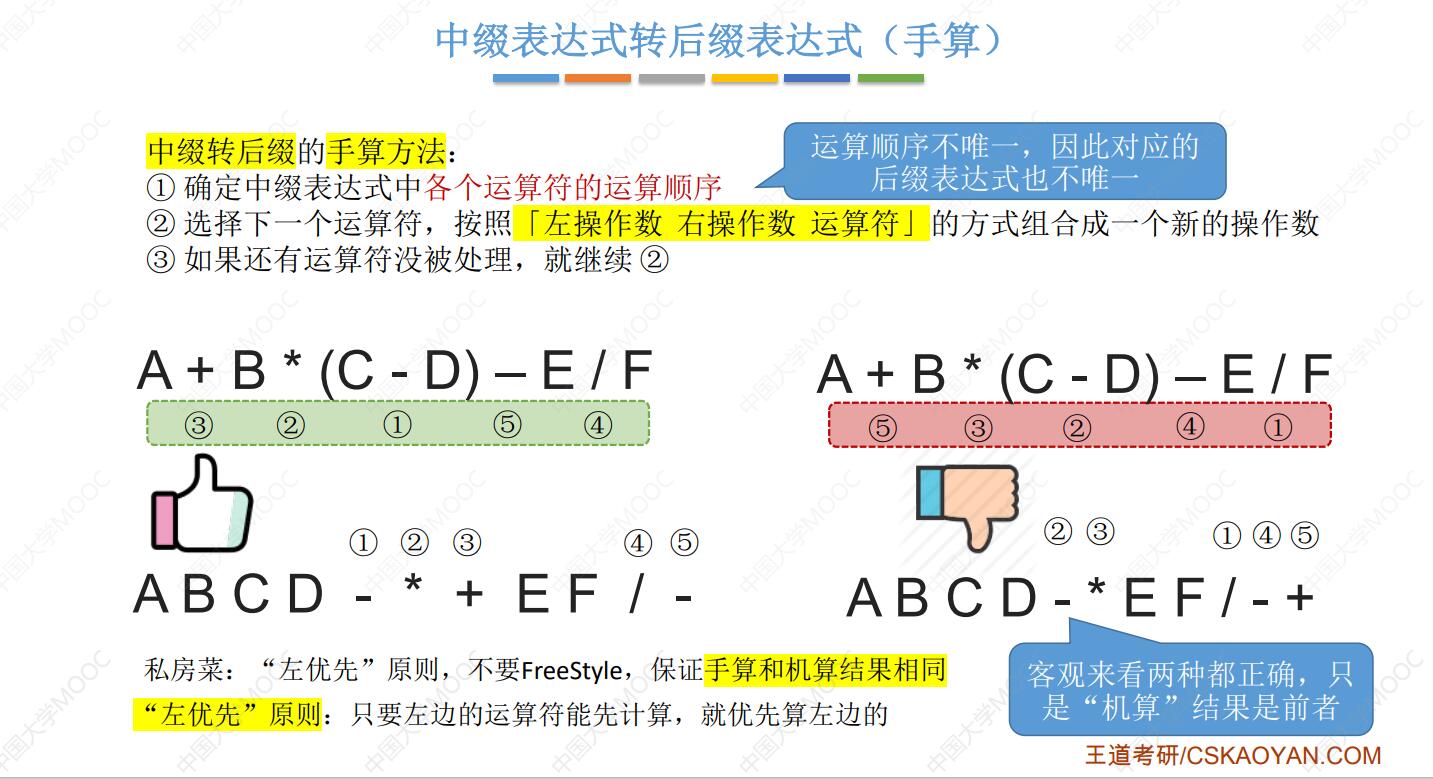
  • 中缀表达式转为后缀表达式
    • 手算（在确定中缀表达式的运算顺序时，只要左边的能算，就优先算左边的）
      • 
    • 机算
      • 
  • 后缀表达式求值
    • 手算
      • 
    • 机算
      • 
• 前缀表达式
  • 定义：也称波兰表达式，运算符在两个操作数的前面（$-+ab*cd$）
  • 中缀表达式转前缀表达式
    • 
  • 前缀表达式求值
    • 

栈在递归中的应用

• 关于函数的调用

  • 函数调用的特点：最后被调用的函数最先执行结束（LIFO）
  • 函数调用时，需要用一个函数调用栈存储相关信息：调用返回地址、实参、局部变量
  • 图片
    • 

• 关于递归

  • 定义：若在一个函数、过程或数据结构的定义中又应用了它自身，则称为递归

    • 递归调用时，函数调用栈可称为”递归工作栈”

    • 每进入一层递归，就将递归调用所需信息压入栈顶

    • 每退出一层递归，就从栈顶弹出相应信息
  • 递归模型不能是循环定义的，必须满足的两个条件：递归表达式（递归体）；边界条件（递归出口）。
  • 适合用“递归”算法解决的问题：可以把原始问题转换为属性相同，但规模较小的问题，此时可以大大减少程序的代码量
  • 可以将递归算法转换为非递归算法，通常需要借助栈来实现这种转换

  • 递归程序的缺点

    • 太多层递归可能会导致栈溢出
    • 通常效率较低，可能包含很多重复计算
    • 空间复杂度较高
  • 消除递归不一定必须用栈来实现

• 求阶乘问题

  • 代码实现

    #include<stdio.h>
    int factorial(int n)
    {
      if(n==0||n==1)//边界条件 
         return 1;
      else
         return n*factorial(n-1);//递归表达式 
    }  
    int main()
    {
     int n=factorial(10);
     printf("%d",n);
     return 0;
    }

  • 图片

    • 

• 斐波那契数列问题

  • 

队列的应用

• 可作为树的层次遍历、图的广度遍历、页面替换算法、可作为数据缓冲区（打印机应用）

4.数组和特殊矩阵（选择题考点✪）

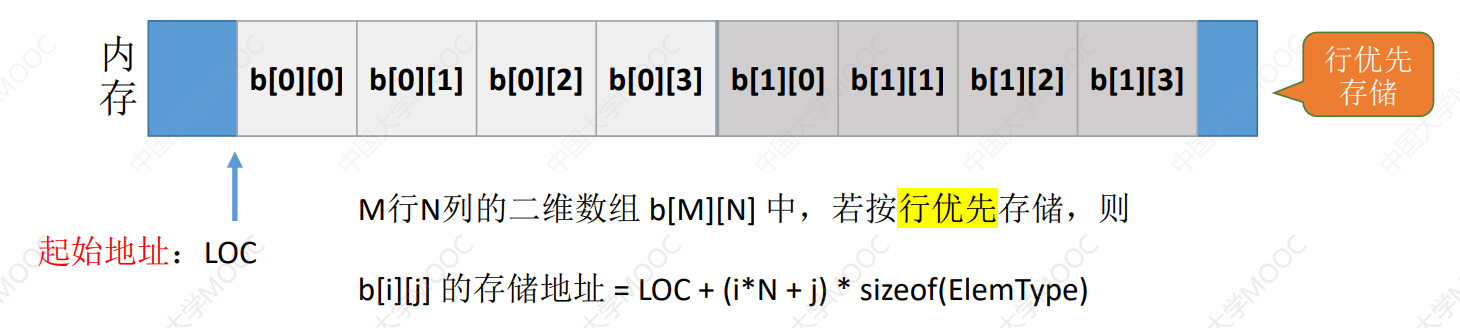
• 数组的存储结构
  • 数组是由n(n≥1)个相同类型的数据元素构成的有限序列，是线性表的推广（顺序存储结构）
  • 广义表采取的是链式存储结构，一个广义表的表尾总是一个广义表
  • 多维数组的两种映射方法
    • 行优先
      • 
    • 列优先
      • 
• 特殊矩阵的压缩存储
  • 压缩存储的定义：指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间。其目的是节省存储空间
  • 特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。
    常见的特殊矩阵有对称矩阵、上（下）三角矩阵、对角矩阵等。
  • 特殊矩阵的压缩存储方法：找出特殊矩阵中值相同的矩阵元素的分布规律，
    把那些呈现规律性分布的、值相同的多个矩阵元素压缩存储到一个存储空间中。
  • 注意: 二维数组 ${A[n][n]}$ 和 ${A[0 \ldots n-1][0 \ldots n-1]}$ 的写法是等价的。
    • 如果数组写为 ${A[1 \ldots n][1 \ldots n]}$, 则说明指定了从下标 1 开始存储元素。
    • 二维数组元素写为 ${a[i][j]}$, 注意数组元素下标 ${i}$ 和 ${j}$ 通常是从 0 开始的。
    • 矩阵元素通常写为 ${a_{i, j}}$ 或 ${a_{(i)(j)}}$, 注意行号 ${i}$ 和列号 ${j}$ 是 从 1 开始的。
• 特殊矩阵（♚）
  • 处理特殊矩阵的方式，一般先找出前i-1行的规律，再将其与第i行相加即可（通过画出具体的方阵图来分析）
  • 对称矩阵
    • 此时n阶方阵中均有：$a_{i,j} = a_{j,i}$，则只需要存放主对角线和下三角形部分。
    • 如果为将下三角部分的元素存入数组的对称矩阵，此时按行优先方式有以下结论
      （前i-1行可由求和公式得出，为上三角形时，i与j互换）
      • 
  • 三角矩阵
    • 下三角形矩阵
      • 上三角区的所有元素均为同一常量。存储完下三角区和主对角线上的元素之后，紧接着存储对角线上方的常量一次
        • 
      • 行优先原则的下标
        • 
    • 上三角形矩阵
      • 行优先原则的下标
        • 
  • 三对角矩阵（带状矩阵）
    • 三对角矩阵中，所有非零元素都集中在以主对角线为中心的三条对角线的区域，其它区域的元素都为0
      当|i-j|>1时，此时为0
      • 
    • 行优先原则的下标
      • 前i-1行共 3(i-1)-1 个元素 （第一行需要减1）
      • $a_{i,j}$是i行第j-i+2个元素，$a_{i,j}$是第2i+j-2个元素
      • 此时数组下标k为k=2i+j-3
    • 如何根据下标求出元素在数组中的具体位置
      • 
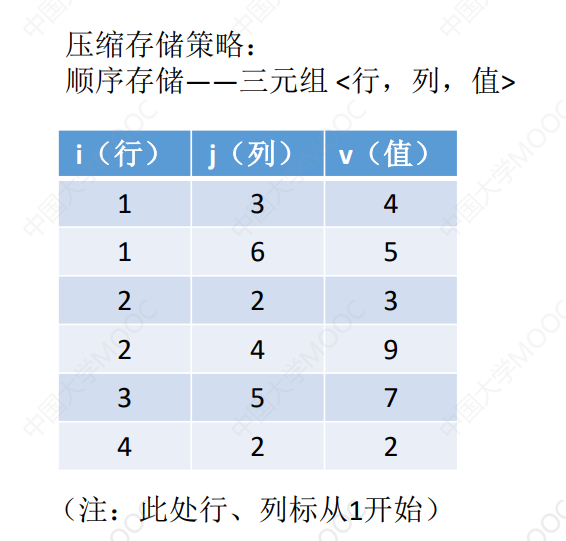
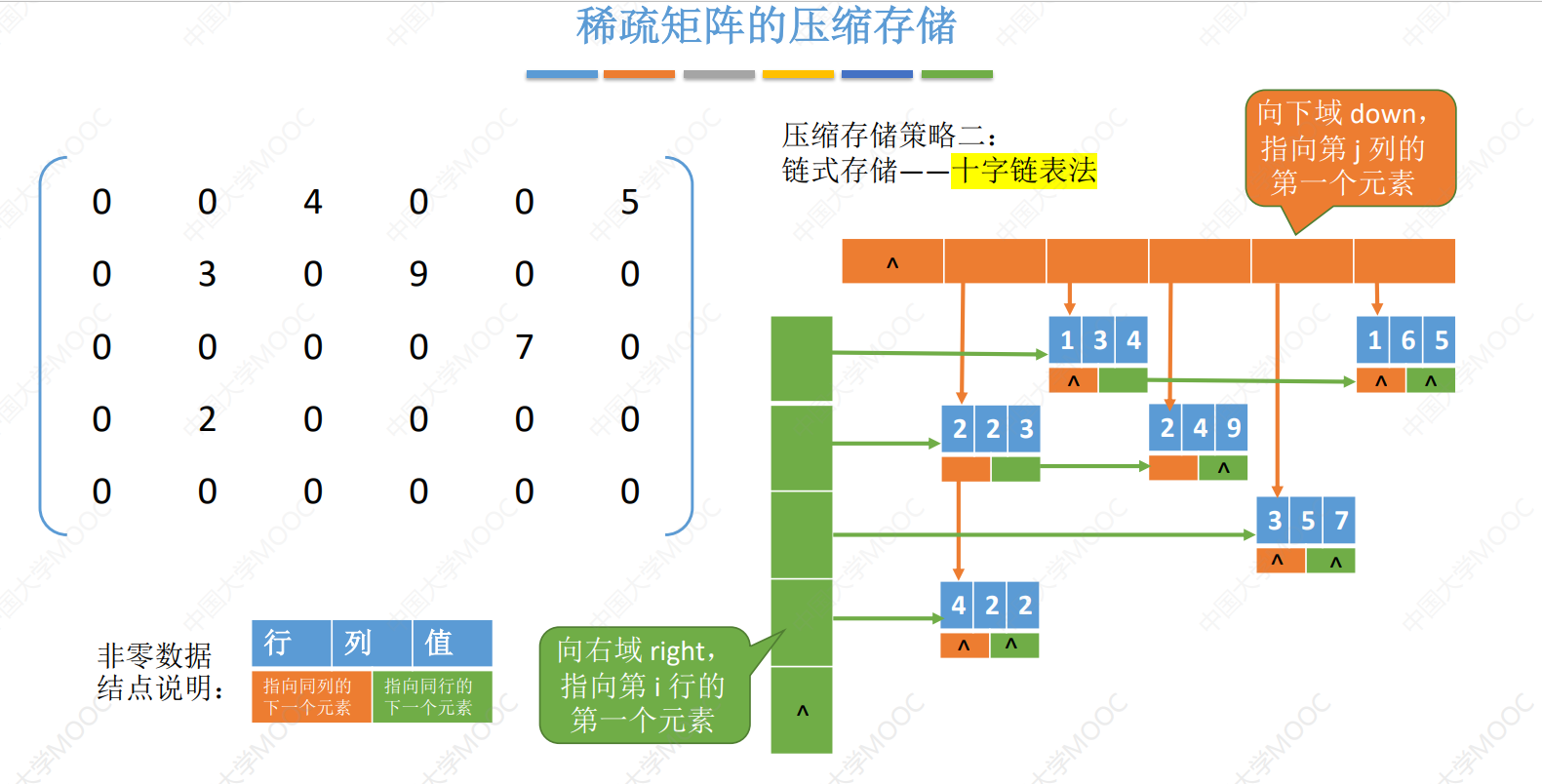
• 稀疏矩阵（压缩存储后必定会失去随机存储的功能）
  • 矩阵中非零元素的个数远远小于为0的元素
  • 使用顺序存储方式压缩存储（三元组表）
    • 
  • 使用链式存储方式压缩存储（十字链表）
    •