数据结构第一章-绪论

发表于 | 更新于: | 分类于 |
字数统计: 5.5k | 阅读时长 ≈ 20 mins.

数据结构第一章 绪论

计算机学科基础：数据结构第一章绪论的学习笔记

1.数据结构的基本概念

  • 数据
  • 数据元素：数据的基本单位，由若干个数据项组成
    数据项是不可分割的最小独立数据单位
  • 数据对象：具有相同性质的数据元素的集合，是数据的一个子集
  • 数据类型：数据类型是一个值的集合和定义在此集合上的一组操作的总称
    • 原子类型：其值不可再分的数据类型。（如bool、int）
    • 结构类型：其值可以再分解为若干成分（分量）的数据类型。(如结构体)
    • 抽象数据类型ADT：抽象数据组织及与之相关的操作
      描述了数据的逻辑结构和抽象运算，定义了一个完整的数据结构，如线性表、栈、队列、树、图等）。
  • 数据结构
    • 数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
      在任何问题中，数据元素都不是孤立存在的，它们之间存在某种关系，这种数据元素相互之间的关系称为结构(Structure)
    • 数据结构包括三方面的内容：逻辑结构、存储结构和数据的运算。
    • 数据的逻辑结构和存储结构是密不可分的两个方面，一个算法的设计取决于所选定的逻辑结构，
      而算法的实现依赖于所采用的存储结构。

2.数据结构的三要素

  • 数据的逻辑结构：数据元素之间的逻辑关系，数据的逻辑结构独立于其存储结构
    • 线性结构（数据元素之间只存在一对一的关系）
      • 一般线性表
      • 受限线性表：栈和队列、串
      • 线性表推广：数组
    • 非线性结构
      • 集合 （结构中的数据元素之间除“同属一个集合外”，别无其他关系）
      • 树形结构：一般树、二叉树（数据元素之间存在一对多的关系）
      • 图状结构：有向图、无向图（数据元素之间存在多对多的关系）
    • 概念型的例题
      • 此题选C，逻辑结构均是线性结构
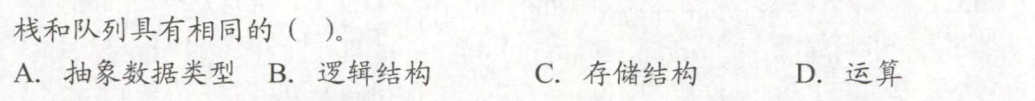
      • pCs0g2t.png
  • 数据的存储结构：存储结构是指数据结构在计算机中的表示（又称映像），也称物理结构。
    包括数据元素的表示和关系的表示（存储数据时，不仅要存储各数据元素的值，也要存储数据元素之间的关系）
    • 顺序存储：把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中（如顺序表）
      元素之间的关系由存储单元的邻接关系来体现。
      • 其优点是可以实现随机存取，每个元素占用最少的存储空间
      • 缺点是只能使用相邻的一整块存储单元，因此可能产生较多的外部碎片。
    • 链式存储：不要求逻辑上相邻的元素在物理位置上也相邻，
      借助指示元素存储地址的指针来表示元素之间的逻辑关系
      • 链式存储时，链式存储时各个不同结点的存储空间可以不连续，但结点内的存储单元地址一定连续
      • 链式存储结构比顺序存储结构更能方便地表示各种逻辑结构
      • 其优点是不会出现碎片现象，能充分利用所有存储单元
      • 缺点是每个元素因存储指针而占用额外的存储空间，且只能实现顺序存取。
    • 索引存储：在存储元素信息的同时，还建立附加的索引表。
      索引表中的每项称为索引项，索引项的一般形式是(关键字，地址)。
      • 其优点是检索速度快：缺点是附加的索引表额外占用存储空间。
      • 增加和删除数据时也要修改索引表，因而会花费较多的时间。
    • 散列存储：根据元素的关键字直接计算出该元素的存储地址，又称哈希(Hsh)存储。
      • 其优点是检索、增加和删除结点的操作都很快
      • 缺点是若散列函数不好，则可能出现元素存储单元的冲突，而解决冲突会增加时间和空间开销。
  • 数据的运算：施加在数据上的运算包括运算的定义和实现。
    • 运算的定义是针对逻辑结构的，指出运算的功能
    • 运算的实现是针对存储结构的，指出运算的具体操作步骤。
    • 不是每种数据结构都具备三种基本运算：插入、删除和查找
      如栈和队列无法查找，二维数组无法删除

3.算法的基本概念

  • 算法的概念：对特定问题求解步骤的一种描述，它是指令的有限序列，其中的每条指令表示一个或多个操作。
  • 五个重要特性
    • 有穷性：一个算法必须总在执行有穷步之后结束，且每一步都可在有穷时间内完成
    • 确定性：算法中每条指令必须有确切的含义，对于相同的输入只能得出相同的输出。
    • 可行性：算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
    • 输入：一个算法有零个或多个输入，这些输入取自于某个特定的对象的集合。
    • 输出：一个算法有一个或多个输出，这些输出是与输入有着某种特定关系的量。
  • 四个目标
    • 正确性
    • 可读性
    • 健壮性
    • 高效率与低存储量需求：效率是指算法执行的时间，存储量需求是指算法执行过程中所需要的最大存储空间，
      这两者都与问题的规模有关。

4.算法效率的度量（✪）

  • 时间复杂度

    • 一个语句的频度是指该语句在算法中被重复执行的次数。算法中所有语句的频度之和记为T(n)，
      它是该算法问题规模n的函数，时间复杂度主要分析T(n)的数量级，执行时间与时间复杂度的值成正比。
    • 算法中基本运算（最深层循环内的语句）的频度与T(n)同数量级，
      因此通常采用算法中基本运算的频度f(n)来分析时间复杂度，$T ( n ) = O ( f ( n ) )$
      • 如此题中，问题规模始终都是n，执行时间与时间复杂度的值成正比，选C
        • pCse6aQ.png
      • 此题可以反映时间复杂度是看问题规模的数量级（即看最高阶，抓大头选B）
        • pCsKhY4.png
      • 但是有两个变量的话就不一样了，如此题选C
        • pPMMWOs.png
    • 算法的时间复杂度不仅依赖于问题的规模，也取决于待输入数据的性质（如输入数据元素的初始状态)

  • 空间复杂度：算法的空间复杂度S(n)定义为该算法所耗费的存储空间，它是问题规模n的函数。

  • 关于时间复杂度的例题（♚）

    • 步骤：首先确定循环中变化的值，之后跟据其变化情况列出其经过每轮循环之后的值
      （先用实数，最后写出规律式（含频数k）），之后并与问题规模n组成不等式，最后求出k关于n的表达式
    • 例1
      • 此时写出i的变化规律：$1,2,4…2^{k},2^{k}=n,k=log_{2}n$
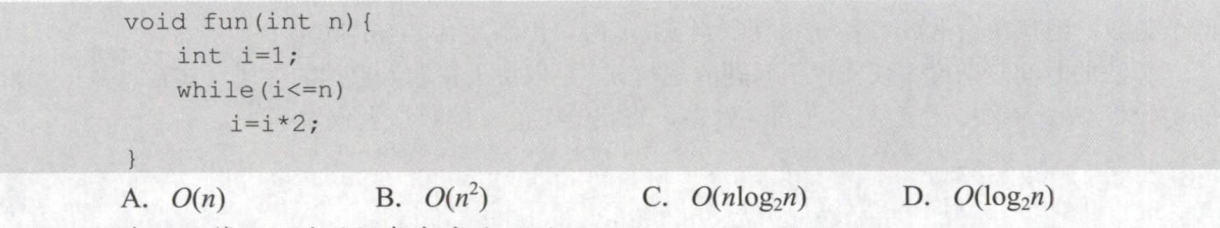
      • pCsnQ0O.png
    • 例2
      • 此时写出x的变化规律：$4,8,16…2^{k+1},2^{k+1}<n/2,k=log_{2}n/2-1=log_{2}n-2$，此时即选A
      • pCsu8bT.png
    • 例3
      • 此时有内外两层的循环，且外层循环的值决定了内层循环的次数，应该以外层为基准来看
      • 外层执行第一轮(i=1)：最内层语句执行2次，外层执行第二轮(i=2)，最内层语句执行4次，
        外层执行第三轮(i=3)，最内层语句执行6次，
      • 此时有规律得（外层执行第n轮时，最内层语句执行2n次）总次数即为相加（求和公式(2+2n)*n/2)=n(n+1)）
      • pCsKneK.png

    • 例4

      • 先看外层的循环取值

      • 此时有$i=1,2,4……2^{k}<n ，此时对应的内层总次数相加为1+2+……2^{k}=2^{k+1}-1<2n$，时间复杂度为n

      • pCs3Arn.png

    • 例5

      • 此时有两层循环但是内层循环的次数不由外层循环的值确定，此时可以看做两个单独的循环，总次数即为此两次循环的积，选C

      • pCsKsln.png

    • 例6

      • 将表达式简化后写出规律，i=0时，sum=1；i=1，sum=1+2，i=2，sum=1+2+3，则i=k时，sum=(1+k)k/2=n，此时选B

      • pCslT6s.png

-------------本文结束-------------